Risk, Reliability, and Resilience Engineering

Overview

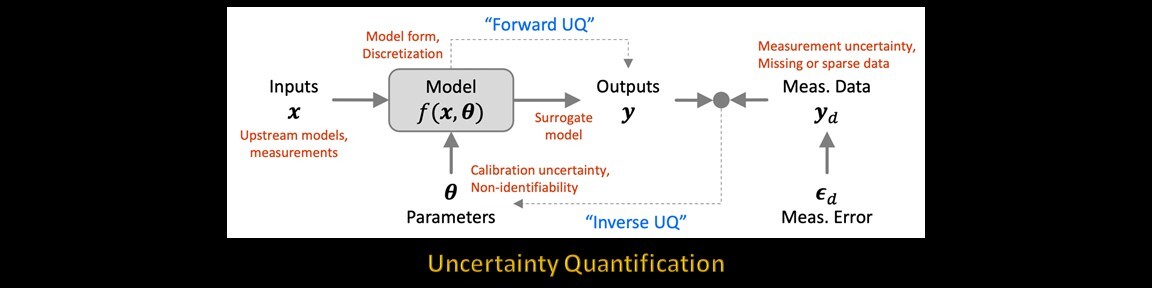
Physics-based models are approximate representations of real-world systems. The complexity of engineering systems means that only limited measurements may be available to establish model accuracy. Due to system complexity and limited measurements, there are assumptions and uncertainty about the model form, approximations in the solution procedure, and uncertainty regarding model inputs, all of which leads to uncertainty in the model output. Uncertainty quantification (UQ) aims to estimate these various sources of uncertainty and the resulting uncertainty in the model prediction. This supports improved model credibility and better decision-making under uncertainty.

The figure below shows several sources of uncertainty. These may also be grouped into aleatory uncertainty (irreducible uncertainty), which is the natural variation of inputs that impact the QoI, and epistemic uncertainty (reducible uncertainty), which results from the lack of knowledge of the system, model, solution method, and measurements.

UQ consists of activities such as model verification, sensitivity analysis, calibration, surrogate modeling, validation, and uncertainty propagation. Forward UQ quantifies uncertainty in the model output given uncertainties in the inputs, model parameters, and model errors. Inverse UQ is related to model calibration which updates model parameter uncertainty using measurements (which are also uncertain).

Current Research

Methodology

1. Efficient sampling algorithms for Bayesian inference
2. Surrogate modeling and Bayesian inference in high-dimensional spaces
3. Bayesian estimation of model error
4. Variance-based sensitivity analysis (Global sensitivity analysis)
5. Model validation with high-dimensional output

Applications

1. UQ for heat transfer in turbine disc
2. UQ for heat transfer in thermal battery
3. UQ in additive manufacturing

Methodology 

1. Efficient sampling algorithms for Bayesian inference

• Limitations in the popular MCMC
  • Computational expense due to serial model evaluations
  • Gets stuck in a single mode of multi-modal distributions

• Proposed Method: IISGA – iterative importance sample with genetic algorithm [1]
  • Computational speedup through parallel computing à iterative importance sampling
  • Infuse robustness: avoid sample degeneracy and explore multi-model distributions à genetic algorithm
  • Address curse of dimensionality due to many calibrated parameters à inflated likelihood

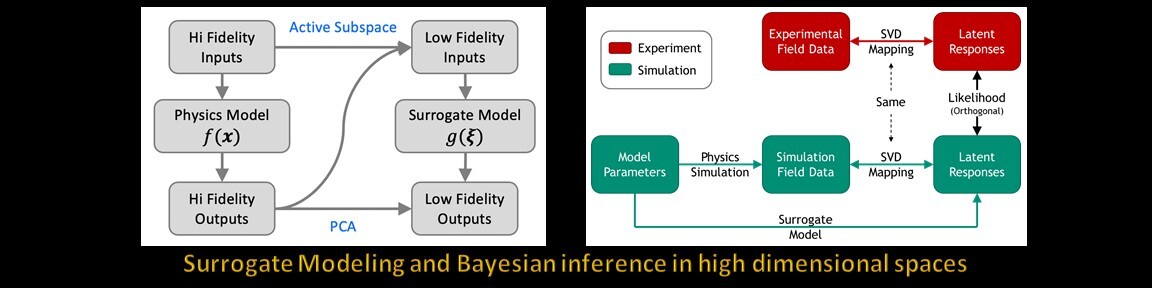
2. Surrogate Modeling and Bayesian inference in high dimensional spaces

• Transform high-dimensional spatio-temporal outputs to low-dimensional, uncorrelated latent space using Singular value decomposition (SVD) [1] or Principal components analysis (PCA) [2]
• Transform high-dimensional inputs using the active subspace (AS) method [2,3], which identifies a subspace of important directions within the gradient space of the model
• The PC-AS method combines these mappings from the physics model to a low-dimensional surrogate model as shown below (first diagram)
• The measured outputs are also transformed into the latent space for comparison to the dimension-reduced surrogate model during Bayesian inference/calibration (second diagram)

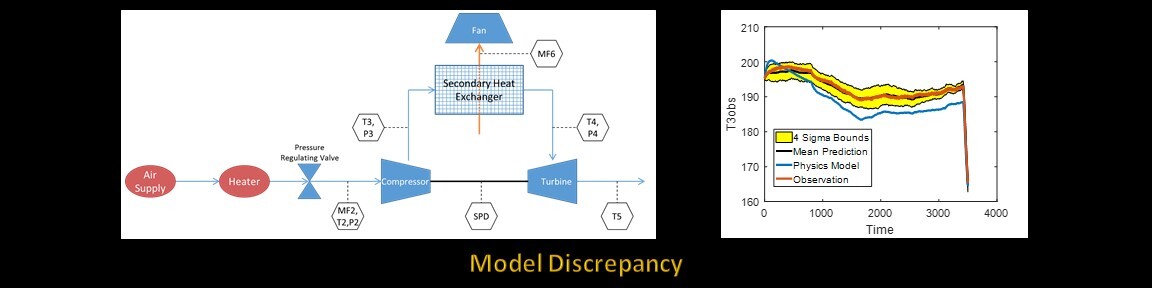
3. Bayesian estimation of model error

1. Model discrepancy (output space)
2. Model form error (governing equation)

3.1. Model discrepancy [4]

• Air cycle machine
  • Cooling on airplanes
  • Complex system to model
    • Thermodynamics
    • Fluid dynamics (compressible fluid)
• Predicted the model discrepancy for a new mission (flight)
  • Use deep learning and available test data to build a model for simulation discrepancy
  • Probabilistic assessment of model reliability

3.2. Model form error [5]

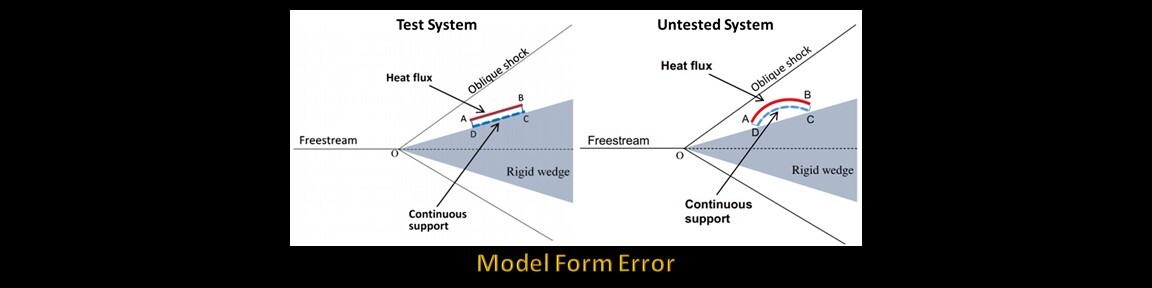
• Model form error (MFE) is the difference between the simulation’s governing equations and the underlying physics
• Model discrepancy is at the level of model output, which is a consequence of model form error
• Prediction requires an extrapolation across one or more of the following: input loadings, system configurations, or output quantities/locations
  • An estimated model discrepancy can be used to locally correct the simulation near the training points where the discrepancy was learned (interpolation only)
  • Model discrepancy cannot be extrapolated, but model form error can be, since it is at the level of governing equations
  • An estimated MFE can correct simulation predictions in extrapolated cases as long as the governing equations still hold

4. Global Sensitivity Analysis

• Aims to provide a quantitative assessment of the relative contribution of each uncertainty source to the uncertainty in the model response
• Expanding GSA to consider both aleatory and epistemic uncertainty sources is beneficial in supporting resource allocation decisions
• If the contribution of epistemic uncertainty is found to be significant, then it may be valuable to collect more data to reduce the epistemic uncertainty and thus its contribution to the output uncertainty
• Developed methodologies for information fusion and machine learning for sensitivity analysis using both physics knowledge and experimental data, while accounting for model uncertainty [6]
  • Several physics-informed machine learning (ML) models were developed by leveraging two strategies for incorporating physics knowledge into ML models:
    • Incorporating physics constraints within the loss functions used in training the ML models, and
    • Pre-training an ML model with simulation data and then updating it with experimental data
• Quantification of the contribution of each uncertainty source to the uncertainty in the quantity of interest; modularized global sensitivity analysis [7] and efficient Gaussian mixture copula (GMC) approximation of the joint distribution for fast computation of sensitivity indices [3, 8].
• Time dependent GSA is performed to quantify the contributions of model parameters at various stages of the physical process [9]

5. Model validation with high-dimensional output

Model validation is the process of determining the degree to which a model is an accurate representation of the real world from the perspective of the intended use of the model. [10,11]

Quantitative validation metrics for model credibility and decision-making:

• High-dimensional model responses and corresponding measurements
  • Time-dependent [12]
  • Multi-dimensional [13]
  • Correlated responses, e.g., field response
• Uncertainty in models and measurements
• Limited measurements

Applications

1. UQ for heat transfer in turbine disc [2]

• A gas turbine heat transfer model application considers limited measurements, multivariate inputs/outputs, and a time-dependent response.
• Combined Principal Components Analysis (PCA) and Active Subspace (AS) dimension reduction methods are used to develop a PC-AS surrogate model.
• Efficient Bayesian calibration uses the PC-AS surrogate to estimate parameter uncertainties.
• The calibration is performed within PC-space (latent space) taking advantage of dimension-reduction and orthogonality.

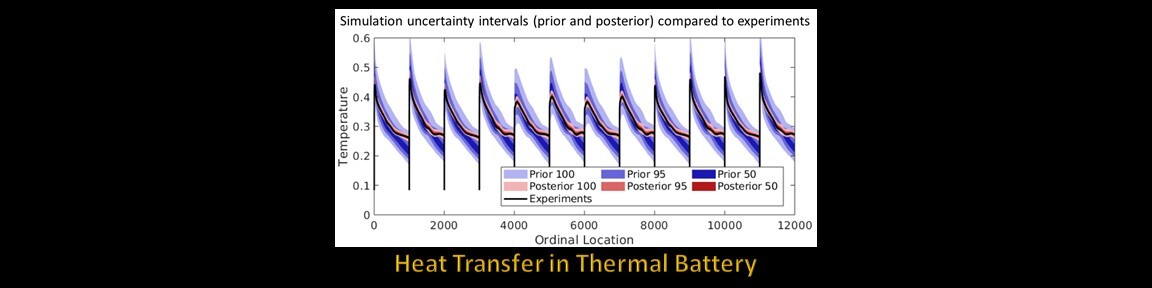
2. UQ for heat transfer in thermal battery [1]

• Batteries operate at very high temperatures
  • Salt electrolyte is melted to activate battery
• Thermocouples capture temperature over space and time
  • Field data responses converted to latent responses using SVD
• Predictive capabilities of the simulation are improved using Bayesian calibration
  • 26 calibration parameters: 16 model parameters, 10 model discrepancy terms
  • IISGA efficiently estimates the posterior distribution

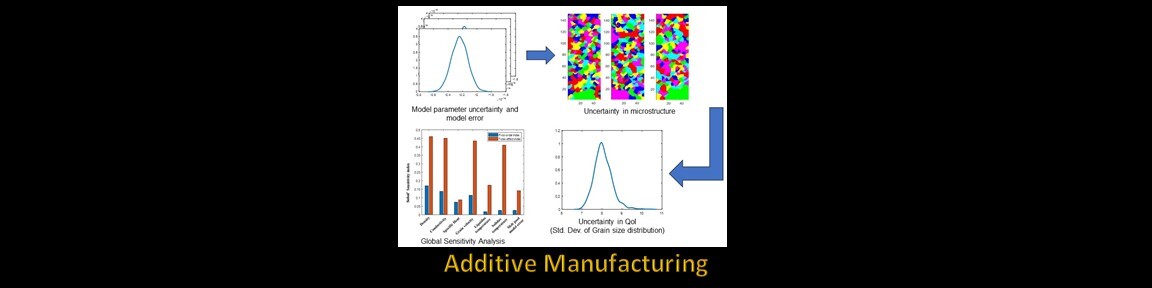
3. UQ in Additive Manufacturing [3,14]

• Modeling of AM process using a multi-scale, multi-physics model to predict the quantity of interest QOI (e.g., heat transfer analysis using a finite element model and grain growth analysis using cellular automata model to predict microstructure)
• High dimensional input and output: Dimension reduction techniques such as active subspace and singular value decomposition
• Construction of surrogate models in the low-dimensional space
• Propagation of uncertainty through multiple computational models to quantify the uncertainty in QOI, e.g., residual stress, part geometry, porosity/voids, grain size distribution, etc.

Funding

Current People

• Sankaran Mahadevan, Professor
• Abhinav Subramanian, Postdoctoral Fellow
• Paromita Nath, Postdoctoral Fellow
• Kyle Neal, Ph.D. Student
• Andrew White, Ph.D. Student
• Berkcan Kapusuzoglu, Ph.D. Student
• Yulin Guo, Ph.D. Student

Publications

1. Neal, K., Schroeder, B., Mullins, J., Subramanian, A., Mahadevan, S., “Robust Importance Sampling for Bayesian Model Calibration with Spatio-Temporal Data.” International Journal of Uncertainty Quantification, Vol. 11, No. 4, pp. 59-80, 2021.
2. A. White, S. Mahadevan, Z. Grey, J. Schmucker, A. Karl, “Efficient calibration of a turbine disc heat transfer model under uncertainty”, AIAA Journal of Thermophysics and Heat Transfer, 2020.
3. Nath, P., Hu, Z., & Mahadevan , S., “Uncertainty quantification of grain morphology in laser direct metal deposition”. Modelling and Simulation in Materials Science and Engineering, Vol. 27, No. 4, 2019.
4. Neal, K., Hu, Z., Mahadevan, S., and Zumberge, J., "Discrepancy Prediction in Dynamical System Models Under Untested Input Histories." ASME Journal of Computational Nonlinear Dynamics, 2019.
5. Subramanian, A., and Mahadevan, S., “Model Error Propagation in Coupled Multiphysics Systems.” AIAA Journal, Vol. 58, No. 5, 2020.
6. Kapusuzoglu, B. and Mahadevan, S., “Information fusion and machine learning for sensitivity analysis using physics knowledge and experimental data”, Reliability Engineering & System Safety, Special Issue on Sensitivity Analysis of Model Outputs, Under Review.
7. Li, C. and Mahadevan, S., “An efficient modularized sample-based method to estimate the first-order Sobol index", Reliability Engineering & System Safety, 153, pp. 110–121, 2016
8. Hu, Z. & Mahadevan, S., “Probability models for data-driven global sensitivity analysis”, Reliability Engineering & System Safety, 187, pp.40-57, 2019
9. Kapusuzoglu B., Sato M., Mahadevan S., Witherell P., “Process Optimization under Uncertainty for Improving the Bond Quality of Polymer Filaments in Fused Filament Fabrication”, Journal of Manufacturing Science and Engineering, 2020 Aug 18:1-46
10. AIAA, AIAA guide for the verification and validation of computational fluid dynamics simulations. American Institute of Aeronautics and Astronautics, AIAA-G-077-1998, Reston, VA, 1998.
11. ASME, Guide for verification and validation in computational solid mechanics. American Society of Mechanical Engineers, ASME Standard V&V 10-2006, New York, NY; 2006.
12. Ao, D., Hu, Z. and Mahadevan, S., “Dynamics Model Validation Using Time-Domain Metrics”, Journal of Verification, Validation and Uncertainty Quantification, 2017
13. Ling, Y. and Mahadevan, S., “Quantitative model validation techniques: New insights”, Reliability Engineering and System Safety, Elsevier, 111, pp. 217–231, 2013
14. Vohra, M., Nath, P., Mahadevan, S., & Lee, Y.T.T., “Fast surrogate modeling using dimensionality reduction in model inputs and field output: Application to additive manufacturing”, Reliability Engineering & System Safety, Vol. 201, 2020.